MD5

History and cryptanalysis

MD5 is one in a series of message digest algorithms designed by Professor Ronald Rivest of MIT (Rivest, 1992). When analytic work indicated that MD5's predecessor MD4 was likely to be insecure, Rivest designed MD5 in 1991 as a secure replacement. (Hans Dobbertin did indeed later find weaknesses in MD4.)

In 1993, Den Boer and Bosselaers gave an early, although limited, result of finding a "pseudo-collision" of the MD5 compression function; that is, two different initialization vectors that produce an identical digest.

In 1996, Dobbertin announced a collision of the compression function of MD5 (Dobbertin, 1996). While this was not an attack on the full MD5 hash function, it was close enough for cryptographers to recommend switching to a replacement, such as SHA-1 or RIPEMD-160.

The size of the hash value (128 bits) is small enough to contemplate a birthday attack. MD5CRK was a distributed project started in March 2004 with the aim of demonstrating that MD5 is practically insecure by finding a collision using a birthday attack.

MD5CRK ended shortly after 17 August 2004, when collisions for the full MD5 were announced by Xiaoyun Wang, Dengguo Feng, Xuejia Lai, and Hongbo Yu.^[7][8] Their analytical attack was reported to take only one hour on an IBM p690 cluster.^[9]

On 1 March 2005, Arjen Lenstra, Xiaoyun Wang, and Benne de Weger demonstrated construction of two X.509 certificates with different public keys and the same MD5 hash value, a demonstrably practical collision.^[10] The construction included private keys for both public keys. A few days later, Vlastimil Klima described an improved algorithm, able to construct MD5 collisions in a few hours on a single notebook computer.^[11] On 18 March 2006, Klima published an algorithm that could find a collision within one minute on a single notebook computer, using a method he calls tunneling.^[12]

Various MD5-related RFC errata have been published. In 2009, the United States Cyber Command used an MD5 hash value of their mission statement as a part of their official emblem.^[13]

On 24 December 2010, Tao Xie and Dengguo Feng announced the first published single-block (512-bit) MD5 collision.^[14] (Previous collision discoveries had relied on multi-block attacks.) For "security reasons", Xie and Feng did not disclose the new attack method. They issued a challenge to the cryptographic community, offering a US$10,000 reward to the first finder of a different 64-byte collision before 1 January 2013. Marc Stevens responded to the challenge and published colliding single-block messages as well as the construction algorithm and sources.^[15]

In 2011 an informational RFC 6151^[16] was approved to update the security considerations in MD5^[17] and HMAC-MD5.^[18]

Security

The security of the MD5 hash function is severely compromised. A collision attack exists that can find collisions within seconds on a computer with a 2.6 GHz Pentium 4 processor (complexity of 2^24.1).^[19] Further, there is also a chosen-prefix collision attack that can produce a collision for two inputs with specified prefixes within seconds, using off-the-shelf computing hardware (complexity 2³⁹).^[20] The ability to find collisions has been greatly aided by the use of off-the-shelf GPUs. On an NVIDIA GeForce 8400GS graphics processor, 16–18 million hashes per second can be computed. An NVIDIA GeForce 8800 Ultra can calculate more than 200 million hashes per second.^[21]

These hash and collision attacks have been demonstrated in the public in various situations, including colliding document files^[22][23] and digital certificates.^[24] As of 2015, MD5 was demonstrated to be still quite widely used, most notably by security research and antivirus companies.^[25]

As of 2019, one quarter of widely used content management systems were reported to still use MD5 for password hashing.^[6]

Overview of security issues

In 1996, a flaw was found in the design of MD5. While it was not deemed a fatal weakness at the time, cryptographers began recommending the use of other algorithms, such as SHA-1, which has since been found to be vulnerable as well.^[26] In 2004 it was shown that MD5 is not collision-resistant.^[27] As such, MD5 is not suitable for applications like SSL certificates or digital signatures that rely on this property for digital security. Also in 2004 researchers discovered more serious flaws in MD5, and described a feasible collision attack -- a method to create a pair of inputs for which MD5 produces identical checksums.^[7][28] Further advances were made in breaking MD5 in 2005, 2006, and 2007.^[29] In December 2008, a group of researchers used this technique to fake SSL certificate validity.^[24][30]

As of 2010, the CMU Software Engineering Institute considers MD5 "cryptographically broken and unsuitable for further use",^[31] and most U.S. government applications now require the SHA-2 family of hash functions.^[32] In 2012, the Flame malware exploited the weaknesses in MD5 to fake a Microsoft digital signature.^[33]

Collision vulnerabilities

In 1996, collisions were found in the compression function of MD5, and Hans Dobbertin wrote in the RSA Laboratories technical newsletter, "The presented attack does not yet threaten practical applications of MD5, but it comes rather close ... in the future MD5 should no longer be implemented ... where a collision-resistant hash function is required."^[34]

In 2005, researchers were able to create pairs of PostScript documents^[35] and X.509 certificates^[36] with the same hash. Later that year, MD5's designer Ron Rivest wrote that "md5 and sha1 are both clearly broken (in terms of collision-resistance)".^[37]

On 30 December 2008, a group of researchers announced at the 25th Chaos Communication Congress how they had used MD5 collisions to create an intermediate certificate authority certificate that appeared to be legitimate when checked by its MD5 hash.^[24] The researchers used a cluster of Sony PlayStation 3 units at the EPFL in Lausanne, Switzerland^[38] to change a normal SSL certificate issued by RapidSSL into a working CA certificate for that issuer, which could then be used to create other certificates that would appear to be legitimate and issued by RapidSSL. VeriSign, the issuers of RapidSSL certificates, said they stopped issuing new certificates using MD5 as their checksum algorithm for RapidSSL once the vulnerability was announced.^[39] Although Verisign declined to revoke existing certificates signed using MD5, their response was considered adequate by the authors of the exploit (Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, and Benne de Weger).^[24] Bruce Schneier wrote of the attack that "we already knew that MD5 is a broken hash function" and that "no one should be using MD5 anymore".^[40] The SSL researchers wrote, "Our desired impact is that Certification Authorities will stop using MD5 in issuing new certificates. We also hope that use of MD5 in other applications will be reconsidered as well."^[24]

In 2012, according to Microsoft, the authors of the Flame malware used an MD5 collision to forge a Windows code-signing certificate.^[33]

MD5 uses the Merkle–Damgård construction, so if two prefixes with the same hash can be constructed, a common suffix can be added to both to make the collision more likely to be accepted as valid data by the application using it. Furthermore, current collision-finding techniques allow to specify an arbitrary prefix: an attacker can create two colliding files that both begin with the same content. All the attacker needs to generate two colliding files is a template file with a 128-byte block of data, aligned on a 64-byte boundary, that can be changed freely by the collision-finding algorithm. An example MD5 collision, with the two messages differing in 6 bits, is:

d131dd02c5e6eec4 693d9a0698aff95c 2fcab58712467eab 4004583eb8fb7f89
55ad340609f4b302 83e488832571415a 085125e8f7cdc99f d91dbdf280373c5b
d8823e3156348f5b ae6dacd436c919c6 dd53e2b487da03fd 02396306d248cda0
e99f33420f577ee8 ce54b67080a80d1e c69821bcb6a88393 96f9652b6ff72a70

d131dd02c5e6eec4 693d9a0698aff95c 2fcab50712467eab 4004583eb8fb7f89
55ad340609f4b302 83e4888325f1415a 085125e8f7cdc99f d91dbd7280373c5b
d8823e3156348f5b ae6dacd436c919c6 dd53e23487da03fd 02396306d248cda0
e99f33420f577ee8 ce54b67080280d1e c69821bcb6a88393 96f965ab6ff72a70

Both produce the MD5 hash 79054025255fb1a26e4bc422aef54eb4.^[41] The difference between the two samples is that the leading bit in each nibble has been flipped. For example, the 20th byte (offset 0x13) in the top sample, 0x87, is 10000111 in binary. The leading bit in the byte (also the leading bit in the first nibble) is flipped to make 00000111, which is 0x07, as shown in the lower sample.

Later it was also found to be possible to construct collisions between two files with separately chosen prefixes. This technique was used in the creation of the rogue CA certificate in 2008. A new variant of parallelized collision searching using MPI was proposed by Anton Kuznetsov in 2014, which allowed to find a collision in 11 hours on a computing cluster.^[42]

Preimage vulnerability

In April 2009, an attack against MD5 was published that breaks MD5's preimage resistance. This attack is only theoretical, with a computational complexity of 2^123.4 for full preimage.^[43][44]

Applications

MD5 digests have been widely used in the software world to provide some assurance that a transferred file has arrived intact. For example, file servers often provide a pre-computed MD5 (known as md5sum) checksum for the files, so that a user can compare the checksum of the downloaded file to it. Most unix-based operating systems include MD5 sum utilities in their distribution packages; Windows users may use the included PowerShell function "Get-FileHash", install a Microsoft utility,^[45][46] or use third-party applications. Android ROMs also use this type of checksum.

As it is easy to generate MD5 collisions, it is possible for the person who created the file to create a second file with the same checksum, so this technique cannot protect against some forms of malicious tampering. In some cases, the checksum cannot be trusted (for example, if it was obtained over the same channel as the downloaded file), in which case MD5 can only provide error-checking functionality: it will recognize a corrupt or incomplete download, which becomes more likely when downloading larger files.

Historically, MD5 has been used to store a one-way hash of a password, often with key stretching.^[47][48] NIST does not include MD5 in their list of recommended hashes for password storage.^[49]

MD5 is also used in the field of electronic discovery, in order to provide a unique identifier for each document that is exchanged during the legal discovery process. This method can be used to replace the Bates stamp numbering system that has been used for decades during the exchange of paper documents. As above, this usage should be discouraged due to the ease of collision attacks.

Algorithm

Figure 1. One MD5 operation. MD5 consists of 64 of these operations, grouped in four rounds of 16 operations. F is a nonlinear function; one function is used in each round. M_i denotes a 32-bit block of the message input, and K_i denotes a 32-bit constant, different for each operation. <<<_s denotes a left bit rotation by s places; s varies for each operation. ${\displaystyle \boxplus }$ denotes addition modulo 2³².

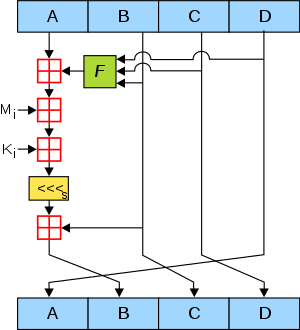
MD5 processes a variable-length message into a fixed-length output of 128 bits. The input message is broken up into chunks of 512-bit blocks (sixteen 32-bit words); the message is padded so that its length is divisible by 512. The padding works as follows: first a single bit, 1, is appended to the end of the message. This is followed by as many zeros as are required to bring the length of the message up to 64 bits fewer than a multiple of 512. The remaining bits are filled up with 64 bits representing the length of the original message, modulo 2⁶⁴.

The main MD5 algorithm operates on a 128-bit state, divided into four 32-bit words, denoted A, B, C, and D. These are initialized to certain fixed constants. The main algorithm then uses each 512-bit message block in turn to modify the state. The processing of a message block consists of four similar stages, termed rounds; each round is composed of 16 similar operations based on a non-linear function F, modular addition, and left rotation. Figure 1 illustrates one operation within a round. There are four possible functions; a different one is used in each round:

${\displaystyle {\begin{aligned}F(B,C,D)&=(B\wedge {C})\vee (\neg {B}\wedge {D})\\G(B,C,D)&=(B\wedge {D})\vee (C\wedge \neg {D})\\H(B,C,D)&=B\oplus C\oplus D\\I(B,C,D)&=C\oplus (B\vee \neg {D})\end{aligned}}}$

${\displaystyle \oplus ,\wedge ,\vee ,\neg }$ denote the XOR, AND, OR and NOT operations respectively.

Pseudocode

This section possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (August 2020) (Learn how and when to remove this template message)

The MD5 hash is calculated according to this algorithm.^[50] All values are in little-endian.

// : All variables are unsigned 32 bit and wrap modulo 2^32 when calculating
var int s[64], K[64]
var int i

// s specifies the per-round shift amounts
s[ 0..15] := { 7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22 }
s[16..31] := { 5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20 }
s[32..47] := { 4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23 }
s[48..63] := { 6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21 }

// Use binary integer part of the sines of integers (Radians) as constants:
for i from 0 to 63 do
    K[i] := floor(232 × abs (sin(i + 1)))
end for
// (Or just use the following precomputed table):
K[ 0.. 3] := { 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee }
K[ 4.. 7] := { 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501 }
K[ 8..11] := { 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be }
K[12..15] := { 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821 }
K[16..19] := { 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa }
K[20..23] := { 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8 }
K[24..27] := { 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed }
K[28..31] := { 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a }
K[32..35] := { 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c }
K[36..39] := { 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70 }
K[40..43] := { 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05 }
K[44..47] := { 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665 }
K[48..51] := { 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039 }
K[52..55] := { 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1 }
K[56..59] := { 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1 }
K[60..63] := { 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 }

// Initialize variables:
var int a0 := 0x67452301   // A
var int b0 := 0xefcdab89   // B
var int c0 := 0x98badcfe   // C
var int d0 := 0x10325476   // D

// Pre-processing: adding a single 1 bit
append "1" bit to message    
 // Notice: the input bytes are considered as bits strings,
 //  where the first bit is the most significant bit of the byte.[51]

// Pre-processing: padding with zeros
append "0" bit until message length in bits ≡ 448 (mod 512)
append original length in bits mod 264to message

// Process the message in successive 512-bit chunks:
for each 512-bit chunk of padded message do
    break chunk into sixteen 32-bit words M[j], 0 ≤ j ≤ 15
    // Initialize hash value for this chunk:
    var int A := a0
    var int B := b0
    var int C := c0
    var int D := d0
    // Main loop:
    for i from 0 to 63 do
        var int F, g
        if 0 ≤ i ≤ 15 then
            F := (B and C) or ((not B) and D)
            g := i
        else if 16 ≤ i ≤ 31 then
            F := (D and B) or ((not D) and C)
            g := (5×i + 1) mod 16
        else if 32 ≤ i ≤ 47 then
            F := B xor C xor D
            g := (3×i + 5) mod 16
        else if 48 ≤ i ≤ 63 then
            F := C xor (B or (not D))
            g := (7×i) mod 16
        // Be wary of the below definitions of a,b,c,d
        F := F + A + K[i] + M[g]  // M[g] must be a 32-bits block
        A := D
        D := C
        C := B
        B := B + leftrotate(F, s[i])
    end for
    // Add this chunk's hash to result so far:
    a0 := a0 + A
    b0 := b0 + B
    c0 := c0 + C
    d0 := d0 + D
end for

var char digest[16] := a0 append b0 append c0 append d0 // (Output is in little-endian)

// leftrotate function definition
leftrotate (x, c)
    return (x << c) binary or (x >> (32-c));

Instead of the formulation from the original RFC 1321 shown, the following may be used for improved efficiency (useful if assembly language is being used – otherwise, the compiler will generally optimize the above code. Since each computation is dependent on another in these formulations, this is often slower than the above method where the nand/and can be parallelised):

( 0 ≤ i ≤ 15): F := D xor (B and (C xor D))
(16 ≤ i ≤ 31): F := C xor (D and (B xor C))

MD5 hashes

The 128-bit (16-byte) MD5 hashes (also termed message digests) are typically represented as a sequence of 32 hexadecimal digits. The following demonstrates a 43-byte ASCII input and the corresponding MD5 hash:

MD5("The quick brown fox jumps over the lazy dog") =
9e107d9d372bb6826bd81d3542a419d6

Even a small change in the message will (with overwhelming probability) result in a mostly different hash, due to the avalanche effect. For example, adding a period to the end of the sentence:

MD5("The quick brown fox jumps over the lazy dog.") = 
e4d909c290d0fb1ca068ffaddf22cbd0

The hash of the zero-length string is:

MD5("") = 
d41d8cd98f00b204e9800998ecf8427e

The MD5 algorithm is specified for messages consisting of any number of bits; it is not limited to multiples of eight bits (octets, bytes). Some MD5 implementations such as md5sum might be limited to octets, or they might not support streaming for messages of an initially undetermined length.

Implementations

Below is a list of cryptography libraries that support MD5:

• Botan
• Bouncy Castle
• cryptlib
• Crypto++
• Libgcrypt
• Nettle
• OpenSSL
• wolfSSL

See also

• Comparison of cryptographic hash functions
• Hash function security summary
• HashClash
• MD5Crypt
• md5deep
• md5sum
• MD6
• SHA-1

References

Further reading

• Berson, Thomas A. (1992). "Differential Cryptanalysis Mod 2³² with Applications to MD5". EUROCRYPT. pp. 71–80. ISBN 3-540-56413-6.
• Bert den Boer; Antoon Bosselaers (1993). Collisions for the Compression Function of MD5. Berlin; London: Springer. pp. 293–304. ISBN 978-3-540-57600-6. Unknown parameter |book-title= ignored (help)
• Hans Dobbertin, Cryptanalysis of MD5 compress. Announcement on Internet, May 1996. "CiteSeerX". Citeseer.ist.psu.edu. Retrieved 9 August 2010.
• Dobbertin, Hans (1996). "The Status of MD5 After a Recent Attack". CryptoBytes. 2 (2).
• Xiaoyun Wang; Hongbo Yu (2005). "How to Break MD5 and Other Hash Functions" (PDF). EUROCRYPT. ISBN 3-540-25910-4. Archived from the original (PDF) on 21 May 2009. Retrieved 6 March 2008.

External links

• W3C recommendation on MD5